 Civilian GPS receiver ("GPS navigation device") in a marine application. |
 Automotive navigation system in a taxicab. |
The Global Positioning System (GPS) is a global navigation satellite system (GNSS) developed by the United States Department of Defense and managed by the United States Air Force 50th Space Wing. It is the only fully functional GNSS in the world, can be used freely by anyone, anywhere, and is often used by civilians for navigation purposes. It uses a constellation of between 24 and 32 medium Earth orbit satellites that transmit precise radiowave signals, which allow GPS receivers to determine their current location, the time, and their velocity. Its official name is NAVSTAR GPS. Although NAVSTAR is not an acronym,[1] a few backronyms have been created for it.[2]
Since it became fully operational on April 27, 1995, GPS has become a widely used aid to navigation worldwide, and a useful tool for map-making, land surveying, commerce, scientific uses, tracking and surveillance, and hobbies such as geocaching. Also, the precise time reference is used in many applications including the scientific study of earthquakes and as a required time synchronization method for cellular network protocols such as the IS-95 standard for CDMA.
[edit] History
The first satellite navigation system, Transit, used by the United States Navy, was first successfully tested in 1960. Using a constellation of five satellites, it could provide a navigational fix approximately once per hour. In 1967, the U.S. Navy developed the Timation satellite which proved the ability to place accurate clocks in space, a technology that GPS relies upon. In the 1970s, the ground-based Omega Navigation System, based on signal phase comparison, became the first worldwide radio navigation system.
The design of GPS is based partly on similar ground-based radio navigation systems, such as LORAN and the Decca Navigator developed in the early 1940s, and used during World War II. Additional inspiration for the GPS came when the Soviet Union launched the first man-made satellite, Sputnik in 1957. A team of U.S. scientists led by Dr. Richard B. Kershner were monitoring Sputnik's radio transmissions. They discovered that, because of the Doppler effect, the frequency of the signal being transmitted by Sputnik was higher as the satellite approached, and lower as it continued away from them. They realized that since they knew their exact location on the globe, they could pinpoint where the satellite was along its orbit by measuring the Doppler distortion.
After Korean Air Lines Flight 007 was shot down in 1983 after straying into the USSR's prohibited airspace,[3] President Ronald Reagan issued a directive making GPS freely available for civilian use as a common good.[4] The satellites were launched between 1989 and 1993.
Initially the highest quality signal was reserved for military use, while the signal available for civilian use was intentionally degraded ("Selective Availability", SA). Selective Availability was ended in 2000, improving the precision of civilian GPS from about 100m to about 20m.
Of crucial importance for the function of GPS is the placement of atomic clocks in the satellites, first proposed by Friedwardt Winterberg in 1955.[5] Only then can the required position accuracy be reached.
[edit] Timeline
- In 1972, the US Air Force Central Inertial Guidance Test Facility (Holloman AFB) conducted developmental flight tests of two prototype GPS receivers over White Sands Missile Range, using ground-based pseudo-satellites.
| Block | Launch Period | Satellites launched | Currently in service |
|---|---|---|---|
| I | 1978–1985 | 10+11 | 0 |
| II | 1985–1990 | 9 | 0 |
| IIA | 1990–1997 | 19 | 13 |
| IIR | 1997–2004 | 12+11 | 12 |
| IIR-M | 2005–2009 | 7+12 | 6 |
| IIF | 2009–2011 | 0+102 | 0 |
| IIIA | 2014–? | 0+123 | 0 |
| IIIB | 0+83 | 0 | |
| IIIC | 0+163 | 0 | |
| Total | 59+21+122+363 | 31 | |
| 1Failed 2In preparation 3Planned. (Last update: 16 December 2008) | |||
- In 1978 the first experimental Block-I GPS satellite was launched.
- In 1983, after Soviet interceptor aircraft shot down the civilian airliner KAL 007 that strayed into prohibited airspace due to navigational errors, killing all 269 people on board, U.S. President Ronald Reagan announced that the GPS would be made available for civilian uses once it was completed.[9][10]
- By 1985, ten more experimental Block-I satellites had been launched to validate the concept.
- On February 14, 1989, the first modern Block-II satellite was launched.
- In 1992, the 2nd Space Wing, which originally managed the system, was de-activated and replaced by the 50th Space Wing.
- By December 1993 the GPS achieved initial operational capability.[11]
- By January 17, 1994 a complete constellation of 24 satellites was in orbit.
- Full Operational Capability was declared by NAVSTAR in April 1995.
- In 1996, recognizing the importance of GPS to civilian users as well as military users, U.S. President Bill Clinton issued a policy directive[12] declaring GPS to be a dual-use system and establishing an Interagency GPS Executive Board to manage it as a national asset.
- In 1998, U.S. Vice President Al Gore announced plans to upgrade GPS with two new civilian signals for enhanced user accuracy and reliability, particularly with respect to aviation safety.
- On May 2, 2000 "Selective Availability" was discontinued as a result of the 1996 executive order, allowing users to receive a non-degraded signal globally.
- In 2004, the United States Government signed an agreement with the European Community establishing cooperation related to GPS and Europe's planned Galileo system.
- In 2004, U.S. President George W. Bush updated the national policy and replaced the executive board with the National Executive Committee for Space-Based Positioning, Navigation, and Timing.
- November 2004, QUALCOMM announced successful tests of Assisted-GPS for mobile phones.[13]
- In 2005, the first modernized GPS satellite was launched and began transmitting a second civilian signal (L2C) for enhanced user performance.
- On September 14, 2007, the aging mainframe-based Ground Segment Control System was transitioned to the new Architecture Evolution Plan.[14]
- The most recent launch was on March 15, 2008.[15] The oldest GPS satellite still in operation was launched on November 26, 1990, and became operational on December 10, 1990.[16]
- On May 19, 2009, the U. S. Government Accountability Office issued a report warning that the some GPS satellites could fail as soon as 2010.[17]
- On May 21, 2009, the Air Force Space Command allayed fears of GPS system failure saying "There's only a small risk we will not continue to exceed our performance standard"[18]
[edit] Basic concept of GPS
A GPS receiver calculates its position by precisely timing the signals sent by the GPS satellitesephemeris), and the general system health and rough orbits of all GPS satellites (the almanac). The receiver measures the transit time of each message and computes the distance to each satellite. Geometric trilateration is used to combine these distances with the location of the satellites to determine the receiver's location. The position is displayed, perhaps with a moving map display or latitude and longitude; elevation information may be included. Many GPS units also show derived information such as direction and speed, calculated from position changes. high above the Earth. Each satellite continually transmits messages containing the time the message was sent, precise orbital information (the
It might seem three satellites are enough to solve for position, since space has three dimensions. However, even a very small clock error multiplied by the very large speed of light[19]—the speed at which satellite signals propagate—results in a large positional error. Therefore receivers use four or more satellites to solve for x, y, z, and t, which is used to correct the receiver's clock. While most GPS applications use the computed location only and effectively hide the very accurately computed time, it is used in a few specialized GPS applications such as time transfer, traffic signal timing, and synchronization of cell phone base stations.
Although four satellites are required for normal operation, fewer apply in special cases. If one variable is already known (for example, a ship or plane may have known elevation), a receiver can determine its position using only three satellites. Some GPS receivers may use additional clues or assumptions (such as reusing the last known altitude, dead reckoning, inertial navigation, or including information from the vehicle computer) to give a degraded position when fewer than four satellites are visible (see [20], Chapters 7 and 8 of [21], and [22]).
[edit] Position calculation introduction
To provide an introductory description of how a GPS receiver works, measurement errors will be ignored in this section. Using messages received from a minimum of four visible satellites, a GPS receiver is able to determine the satellite positions and time sent. The x, y, and z components of position and the time sent are designated as ![\left [x_i, y_i, z_i, t_i\right ]](http://upload.wikimedia.org/math/3/6/7/3671904d39496edbe2ffcbaea29c28b1.png) where the subscript i is the satellite number and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received
where the subscript i is the satellite number and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received  , the GPS receiver can compute the indicated transit time,
, the GPS receiver can compute the indicated transit time, 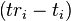 . of the message. Assuming the message traveled at the speed of light, c, the distance traveled,
. of the message. Assuming the message traveled at the speed of light, c, the distance traveled, 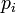 can be computed as
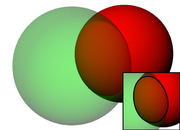
can be computed as  . Knowing the distance from GPS receiver to a satellite and the position of a satellite implies that the GPS receiver is on the surface of a sphere centered at the position of a satellite. Thus we know that the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver will be at an intersection of the surfaces of four spheres. The surfaces of two spheres, if they intersect in more than one point, intersect in a circle. A figure, Two Sphere Surfaces Intersecting in a Circle, is shown below.
. Knowing the distance from GPS receiver to a satellite and the position of a satellite implies that the GPS receiver is on the surface of a sphere centered at the position of a satellite. Thus we know that the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver will be at an intersection of the surfaces of four spheres. The surfaces of two spheres, if they intersect in more than one point, intersect in a circle. A figure, Two Sphere Surfaces Intersecting in a Circle, is shown below.
The article, trilateration, shows mathematically that the surfaces of two spheres, intersecting in more than one point, intersect in a circle.
A circle and sphere surface in most cases of practical interest intersect at two points, although it is conceivable that they could intersect at zero points, one point, or in the very special case in which the centers of the three spheres are colinear (i.e. all three on the same straight line) the sphere surface could intersect the entire circumference of the circle. Another figure, Surface of Sphere Intersecting a Circle (not disk) at Two Points, shows this intersection. The two intersections are marked with dots. Again trilateration clearly shows this mathematically. The correct position of the GPS receiver is the intersection that is closest to the surface of the earth for automobiles and other near-Earth vehicles. The correct position of the GPS receiver is also the intersection which is closest to the surface of the sphere corresponding to the fourth satellite. (The two intersections are symmetrical with respect to the plane containing the three satellites. If the three satellites are not in the same orbital plane, the plane containing the three satellites will not be a vertical plane passing through the center of the Earth. In this case one of the intersections will be closer to the earth than the other. The near-Earth intersection will be the correct position for the case of a near-Earth vehicle. The intersection which is farthest from Earth may be the correct position for space vehicles.)
[edit] Correcting a GPS receiver's clock
The method of calculating position for the case of no errors has been explained. One of the most significant error sources is the GPS receiver's clock. Because of the very large value of the speed of light, c, the estimated distances from the GPS receiver to the satellites, the pseudoranges, are very sensitive to errors in the GPS receiver clock. This suggests that an extremely accurate and expensive clock is required for the GPS receiver to work. On the other hand, manufacturers prefer to build inexpensive GPS receivers for mass markets. The solution for this dilemma is based on the way sphere surfaces intersect in the GPS problem.
It is likely that the surfaces of the three spheres intersect, since the circle of intersection of the first two spheres is normally quite large, and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three, since any clock error could cause it to miss intersecting a point. However, the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let  denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let
denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let 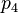 denote the pseudorange of the fourth satellite. Let
denote the pseudorange of the fourth satellite. Let  . Note that
. Note that  is the distance from the computed GPS receiver position to the surface of the sphere corresponding to the fourth satellite. Thus the quotient,
is the distance from the computed GPS receiver position to the surface of the sphere corresponding to the fourth satellite. Thus the quotient,  , provides an estimate of
, provides an estimate of
- (correct time) - (time indicated by the receiver's on-board clock),
and the GPS receiver clock can be advanced if  is positive or delayed if
is positive or delayed if  is negative.
is negative.
[edit] System detail
[edit] System segmentation
The current GPS consists of three major segments. These are the space segment (SS), a control segment (CS), and a user segment (US).[23]
[edit] Space segment
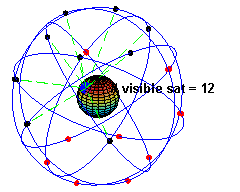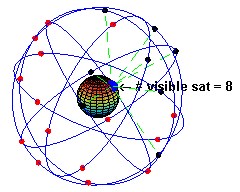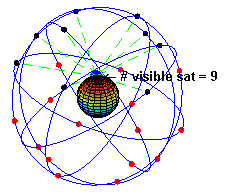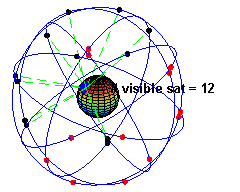
The space segment (SS) comprises the orbiting GPS satellites, or Space Vehicles (SV) in GPS parlance. The GPS design originally called for 24 SVs, eight each in three circular orbital planes,[24] but this was modified to six planes with four satellites each.[25] The orbital planes are centered on the Earth, not rotating with respect to the distant stars.[26] The six planes have approximately 55° inclination (tilt relative to Earth's equator) and are separated by 60° right ascension of the ascending node (angle along the equator from a reference point to the orbit's intersection).[27] The orbits are arranged so that at least six satellites are always within line of sight from almost everywhere on Earth's surface.[28]
Orbiting at an altitude of approximately 20,200 kilometers about 10 satellites are visible within line of sight (12,900 miles or 10,900 nautical miles; orbital radius of 26,600 km (16,500 mi or 14,400 NM)), each SV makes two complete orbits each sidereal day.[29] The ground track of each satellite therefore repeats each (sidereal) day. This was very helpful during development, since even with just four satellites, correct alignment means all four are visible from one spot for a few hours each day. For military operations, the ground track repeat can be used to ensure good coverage in combat zones.
As of March 2008,[30] there are 31 actively broadcasting satellites in the GPS constellation, and two older, retired from active service satellites kept in the constellation as orbital spares. The additional satellites improve the precision of GPS receiver calculations by providing redundant measurements. With the increased number of satellites, the constellation was changed to a nonuniform arrangement. Such an arrangement was shown to improve reliability and availability of the system, relative to a uniform system, when multiple satellites fail.[31][update]
[edit] Control segment
The flight paths of the satellites are tracked by US Air Force monitoring stations in Hawaii, Kwajalein, Ascension Island, Diego Garcia, and Colorado Springs, Colorado, along with monitor stations operated by the National Geospatial-Intelligence Agency (NGA).[32] The tracking information is sent to the Air Force Space Command's master control station at Schriever Air Force Base in Colorado Springs, which is operated by the 2nd Space Operations Squadron (2 SOPS) of the United States Air Force (USAF). Then 2 SOPS contacts each GPS satellite regularly with a navigational update (using the ground antennas at Ascension Island, Diego Garcia, Kwajalein, and Colorado Springs). These updates synchronize the atomic clocks on board the satellites to within a few nanoseconds of each other, and adjust the ephemeris of each satellite's internal orbital model. The updates are created by a Kalman filter which uses inputs from the ground monitoring stations, space weather information, and various other inputs.[33]
Satellite maneuvers are not precise by GPS standards. So to change the orbit of a satellite, the satellite must be marked 'unhealthy', so receivers will not use it in their calculation. Then the maneuver can be carried out, and the resulting orbit tracked from the ground. Then the new ephemeris is uploaded and the satellite marked healthy again.
[edit] User segment
The user's GPS receiver is the user segment (US) of the GPS. In general, GPS receivers are composed of an antenna, tuned to the frequencies transmitted by the satellites, receiver-processors, and a highly-stable clock (often a crystal oscillator). They may also include a display for providing location and speed information to the user. A receiver is often described by its number of channels: this signifies how many satellites it can monitor simultaneously. Originally limited to four or five, this has progressively increased over the years so that, as of 2007, receivers typically have between 12 and 20 channels.[34][update]

GPS receivers may include an input for differential corrections, using the RTCM SC-104 format. This is typically in the form of a RS-232 port at 4,800 bit/s speed. Data is actually sent at a much lower rate, which limits the accuracy of the signal sent using RTCM. Receivers with internal DGPS receivers can outperform those using external RTCM data. As of 2006, even low-cost units commonly include Wide Area Augmentation System (WAAS) receivers.
Many GPS receivers can relay position data to a PC or other device using the NMEA 0183NMEA 2000.[35] Although these protocols are officially defined by the NMEA,[36] references to these protocols have been compiled from public records, allowing open source tools like gpsd to read the protocol without violating intellectual property laws. Other proprietary protocols exist as well, such as the SiRF and MTK protocols. Receivers can interface with other devices using methods including a serial connection, USB or Bluetooth. protocol, or the newer and less widely used
[edit] Navigation signals
Each GPS satellite continuously broadcasts a Navigation Message at 50 bit/s giving the time-of-week, GPS week number and satellite health information (all transmitted in the first part of the message), an ephemeris (transmitted in the second part of the message) and an almanac (later part of the message). The messages are sent in frames, each taking 30 seconds to transmit 1500 bits.
Transmission of each 30 second frame begins precisely on the minute and half minute as indicated by the satellite's atomic clock according to Satellite message format. Each frame contains 5 subframes of length 6 seconds and with 300 bits. Each subframe contains 10 words of 30 bits with length 0.6 seconds each.
Words 1 and 2 of every subframe have the same type of data. The first word is the telemetry word which indicates the beginning of a subframe and is used by the receiver to synch with the navigation message. The second word is the HOW or handover word and it contains timing information which enables the receiver to identify the subframe and provides the time the next subframe was sent.
Words 3 through 10 of subframe 1 contain data describing the satellite clock and its relationship to GPS time. Words 3 through 10 of subframes 2 and 3, contain the ephemeris data, giving the satellite's own precise orbit. The ephemeris is updated every 2 hours and is generally valid for 4 hours, with provisions for updates every 6 hours or longer in non-nominal conditions. The time needed to acquire the ephemeris is becoming a significant element of the delay to first position fix, because, as the hardware becomes more capable, the time to lock onto the satellite signals shrinks, but the ephemeris data requires 30 seconds (worst case) before it is received, due to the low data transmission rate.
The almanac consists of coarse orbit and status information for each satellite in the constellation, an ionospheric model, and information to relate GPS derived time to Coordinated Universal Time (UTC). Words 3 through 10 of subframes 4 and 5 contain a new part of the almanac. Each frame contains 1/25th of the almanac, so 12.5 minutes are required to receive the entire almanac from a single satellite.[37] The almanac serves several purposes. The first is to assist in the acquisition of satellites at power-up by allowing the receiver to generate a list of visible satellites based on stored position and time, while an ephemeris from each satellite is needed to compute position fixes using that satellite. In older hardware, lack of an almanac in a new receiver would cause long delays before providing a valid position, because the search for each satellite was a slow process. Advances in hardware have made the acquisition process much faster, so not having an almanac is no longer an issue. The second purpose is for relating time derived from the GPS (called GPS time) to the international time standard of UTC. Finally, the almanac allows a single-frequency receiver to correct for ionospheric error by using a global ionospheric model. The corrections are not as accurate as augmentation systems like WAAS or dual-frequency receivers. However, it is often better than no correction, since ionospheric error is the largest error source for a single-frequency GPS receiver. An important thing to note about navigation data is that each satellite transmits not only its own ephemeris, but transmits an almanac for all satellites.
All satellites broadcast at the same two frequencies, 1.57542 GHz (L1 signal) and 1.2276 GHz (L2 signal). The receiver can distinguish the signals from different satellites because GPS uses a code division multiple access (CDMA) spread-spectrum technique where the low-bitrate message data is encoded with a high-rate pseudo-random (PRN) sequence that is different for each satellite. The receiver knows the PRN codes for each satellite and can use this to reconstruct the actual message data. The message data is transmitted at 50 bits per second. Two distinct CDMA encodings are used: the coarse/acquisition (C/A) code (a so-called Gold code) at 1.023 million chips per second, and the precise (P) code at 10.23 million chips per second. The L1 carrier is modulated by both the C/A and P codes, while the L2 carrier is only modulated by the P code.[38] The C/A code is public and used by civilian GPS receivers, while the P code can be encrypted as a so-called P(Y) code which is only available to military equipment with a proper decryption key. Both the C/A and P(Y) codes impart the precise time-of-day to the user.
[edit] Satellite frequencies
- L1 (1575.42 MHz): Mix of Navigation Message, coarse-acquisition (C/A) code and encrypted precision P(Y) code, plus the new L1C on future Block III satellites.
- L2 (1227.60 MHz): P(Y) code, plus the new L2C code on the Block IIR-M and newer satellites.
- L3 (1381.05 MHz): Used by the Nuclear Detonation (NUDET) Detection System Payload (NDS) to signal detection of nuclear detonations and other high-energy infrared events. Used to enforce nuclear test ban treaties.
- L4 (1379.913 MHz): Being studied for additional ionospheric correction.
- L5 (1176.45 MHz): Proposed for use as a civilian safety-of-life (SoL) signal (see GPS modernization). This frequency falls into an internationally protected range for aeronautical navigation, promising little or no interference under all circumstances. The first Block IIF satellite that would provide this signal is set to be launched in 2009.[39]
[edit] C/A code
[edit] Demodulation and decoding
Since all of the satellite signals are modulated onto the same L1 carrier frequency, there is a need to separate the signals after demodulation. This is done by assigning each satellite a unique pseudorandom sequence known as a Gold code, and the signals are decoded, after demodulation, using modulo 2 addition of the Gold codes corresponding to satellites n1 through nk, where k is the number of channels in the GPS receiver and n1 through nk are the pseudorandom numbers associated with the satellites. The results of these modulo 2 additions are the 50 bit/s navigation messages from satellites n1 through nk. The Gold codes used in GPS are a sequence of 1023 bits with a period of one millisecond. These Gold codes are highly mutually orthogonal, so that it is unlikely that one satellite signal will be misinterpreted as another. As well, the Gold codes have good auto-correlation properties.[40]
There are 1025 different Gold codes of length 1023 bits, but only 32 are used. These Gold codes are quite often referred to as pseudo random noise since they contain no data and are said to look like random sequences[41]. However, this may be misleading since they are actually deterministic sequences.
If the almanac information has previously been acquired, the receiver picks which satellites to listen for by their PRNs. If the almanac information is not in memory, the receiver enters a search mode and cycles through the PRN numbers until a lock is obtained on one of the satellites. To obtain a lock, it is necessary that there be an unobstructed line of sight from the receiver to the satellite. The receiver can then acquire the almanac and determine the satellites it should listen for. As it detects each satellite's signal, it identifies it by its distinct C/A code pattern.
The receiver uses the C/A Gold code with the same PRN number as the satellite to compute an offset, O, that generates the best correlation. The offset, O, is computed in a trial and error manner. The 1023 bits of the satellite PRN signal are compared with the receiver PRN signal. If correlation is not achieved, the 1023 bits of the receiver's internally generated PRN code are shifted by one bit relative to the satellite's PRN code and the signals are again compared. This process is repeated until correlation is achieved or all 1023 possible cases have been tried.[42] If all 1023 cases have been tried without achieving correlation, the frequency oscillator is offset to the next value and the process is repeated.
Since the carrier frequency received can vary due to Doppler shift, the points where received PRN sequences begin may not differ from O by an exact integral number of milliseconds. Because of this, carrier frequency tracking along with PRN code tracking are used to determine when the received satellite's PRN code begins.[42] Unlike the earlier computation of offset in which trials of all 1023 offsets could potentially be required, the tracking to maintain lock usually requires shifting of half a pulse width or less. To perform this tracking, the receiver observes two quantities, phase error and received frequency offset. The correlation of the received PRN code with respect to the receiver generated PRN code is computed to determine if the bits of the two signals are misaligned. Comparisons with correlation computed with receiver generated PRN code shifted half a pulse width early and half a pulse width late (see section 1.4.2.4 of [21]) are used to estimate adjustment required. The amount of adjustment required for maximum correlation is used in estimating phase error. Received frequency offset from the frequency generated by the receiver provides an estimate of phase rate error. The command for the frequency generator and any further PRN code shifting required are computed as a function of the phase error and the phase rate error in accordance with the control law used. The Doppler velocity is computed as a function of the frequency offset from the carrier nominal frequency. The Doppler velocity is the velocity component along the line of sight of the receiver relative to the satellite.
As the receiver continues to read successive PRN sequences, it will encounter a sudden change in the phase of the 1023 bit received PRN signal. This indicates the beginning of a data bit of the navigation message (see section 1.4.2.5 of [21]). This enables the receiver to begin reading the 20 millisecond bits of the navigation message. Each subframe of the navigation frame begins with a Telemetry Word which enables the receiver to detect the beginning of a subframe and determine the receiver clock time at which the navigation subframe begins. Also each subframe of the navigation frame is identified by bits in the handover word (HOW) thereby enabling the receiver to determine which subframe (see section 1.4.2.6 of [21] and section 2.5.4 of "Essentials of Satellite Navigation Compendium"). There can be a delay of up to 30 seconds before the first estimate of position because of the need to read the ephemeris data before computing the intersections of sphere surfaces.
After a subframe has been read and interpreted, the time the next subframe was sent can be calculated through the use of the clock correction data and the HOW. The receiver knows the receiver clock time of when the beginning of the next subframe was received from detection of the Telemetry Word thereby enabling computation of the transit time and thus the pseudorange. The receiver is potentially capable of getting a new pseudorange measurement at the beginning of each subframe or every 6 seconds.
Then the orbital position data, or ephemeris, from the navigation message is used to calculate precisely where the satellite was at the start of the message. A more sensitive receiver will potentially acquire the ephemeris data more quickly than a less sensitive receiver, especially in a noisy environment.[43]
This process is repeated for each satellite to which the receiver is listening.
[edit] Carrier phase tracking (surveying)
Utilizing the navigation message to measure pseudorange has been discussed. Another method that is used in GPS surveying applications is carrier phase tracking. The period of the carrier frequency times the speed of light gives the wave length, which is about 0.19 meters for the L1 carrier. With a 1% of wave length accuracy in detecting the leading edge, this component of pseudorange error might be as low as 2 millimeters. This compares to 3 meters for the C/A code and 0.3 meters for the P code.
However, this 2 millimeter accuracy requires measuring the total phase, that is the total number of wave lengths plus the fractional wavelength. This requires specially equipped receivers. This method has many applications in the field of surveying.
We now describe a method which could potentially be used to estimate the position of receiver 2 given the position of receiver 1 using triple differencing followed by numerical root finding, and a mathematical technique called least squares. A detailed discussion of the errors is omitted in order to avoid detracting from the description of the methodology. In this description differences are taken in the order of differencing between satellites, differencing between receivers, and differencing between epochs. This should not be construed to mean that this is the only order which can be used. Indeed other orders of taking differences are equally valid.
The satellite carrier total phase can be measured with ambiguity as to the number of cycles as described in CARRIER PHASE MEASUREMENT and CARRIER BEAT PHASE. Let 
 . This notation has been chosen so as to make it clear what the subscripts i, j, and k mean. In view of the fact that the receiver, satellite, and time come in alphabetical order as arguments of
. This notation has been chosen so as to make it clear what the subscripts i, j, and k mean. In view of the fact that the receiver, satellite, and time come in alphabetical order as arguments of 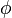 and to strike a balance between readability and conciseness, let
and to strike a balance between readability and conciseness, let  so as to have a concise abbreviation. Also we define three functions, :
so as to have a concise abbreviation. Also we define three functions, :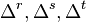 which perform differences between receivers, satellites, and time points respectively. Each of these functions has a linear combination of variables with three subscripts as its argument. These three functions are defined below. If
which perform differences between receivers, satellites, and time points respectively. Each of these functions has a linear combination of variables with three subscripts as its argument. These three functions are defined below. If  is a function of the three integer arguments, i, j, and k then it is a valid argument for the functions, :
is a function of the three integer arguments, i, j, and k then it is a valid argument for the functions, :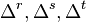 , with the values defined as denote the phase of the carrier of satellite j measured by receiver i at time
, with the values defined as denote the phase of the carrier of satellite j measured by receiver i at time
 ,
, , and
, and .
.
Also if 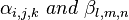 are valid arguments for the three functions and a
are valid arguments for the three functions and a










Tidak ada komentar:
Posting Komentar